One adage that I keep telling myself is as stated in the title above: Practice makes perfect. Want to be good at computer programming? Practice! Want to be good in writing articles? Practice! Want to be good at web development? Taking picture? Problem solving? Practice, practice, practice!
And with my son studying first-grade math now, the same maxim holds true to him as well—”Practice makes perfect, son,” I keep telling him.
Don’t get me wrong; he is good a math. In fact, he is a GATE student, an avid reader with a keen interest for scientific facts, and a future ocean animal scientist slash doctor slash inventor, whatever his final decision be. But still, silly math mistakes happen, and one way to prevent it is to practice more. I had him done more additions and subtractions, and I DO see the result of the drill.
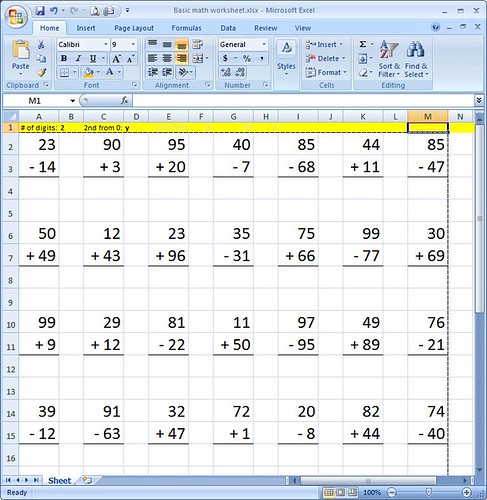
So what tool did I use? Just a simple Excel sheet printout! With formulas, of course—this is a perfect ‘practice’ opportunity for me too, don’t you think?
You can download the Excel file here. Print it out (trust me… it will be easier for your kids to write down the results), refresh the calculation (using F9) or reload the file, and repeat. You can also change the parameters (number of digits, and whether you want the second number to start from 0 or not) to suit your kids’ needs.
The formula
First thing first: Given n as a positive integer, how can we get a list of positive n-digit numbers? Simple: by using the power of 10, the numbers will be from 10n-1 to 10n-1. For example, a list of 2-digit numbers will be from 102-1 to 102-1, or from 10 to 99.
In Excel-speak, this is accomplished using POWER function, where the first parameter is the ‘base’ number (to be powered), and the second parameter is the power*. So for our example above, we can use the formula POWER(10, 2-1) and POWER(10, 2)-1, respectively.
* Please note that Excel also provide a ^ operator you can use intead of the POWER function, ie. a^b is the same as POWER(a,b). However, for the sake of functional clarity, I chose to use POWER function in this article. If you chose ^ operator, go ahead, it will produce the same result, and you’ve earned +1 Coding Achievement along the way! ![]()
Next, having the list of numbers with n digits, how can we pick a random number out of it? RANDBETWEEN to the rescue! Simply provide the lower and upper bounds as its first and second parameter, and this Excel function will happily return us a random number (integers) between those bounds. So far so good?
Alright, so we get the first/initial number of our algebra problem. How to generate the second number?
Again, let’s tackle the easy part first. For addition problems, we can use the same RANDBETWEEN formula as the first number above. Or, if you prefer to have a random number from 0 to n-digit, then we simply supply 0 in the first parameter. That’s it.
How about subtraction problem? Again, use the RANDBETWEEN formula. But since I assume basic math students don’t get the concept of negative numbers yet, this time the random number’s upper bound must be as high as the first number. In other words, if the first number is X, then the second number must be between 0 to X (if we want to start from 0).
Wait—but how can we tell Excel to choose randomly between addition and subtraction? If you’ve come up this far, you should remember that one formula we keep using over and over: The Mighty RANDBETWEEN!!! We can simply ask His Majesty to generate a number between 0 and 1, then treat 0 as subtraction and 1 as addition. This is an Excel-ent way of doing a functional coin flipping, pun intended :D.
So let’s wrap them all up. With the help of the IF function, we can compose an expression like this:
=IF(RANDBETWEEN(0,1) = 0, "- " & RANDBETWEEN(A,B), "+ " & RANDBETWEEN(A,C))
Where:
- A is the lower bound of the problem number, ie. whether starting from 0 or from the first n-digit positive number,
- B is the first number of the subtraction problem, so the calculation won’t involve negative results, and
- C is the upper bound of the addition problem, ie. the last n-digit positive number.
The spreadsheet
Again, you can download the Excel file here. Study it well, grasshopper, as this is one way to practice your Excel-fu. Remember: Practice Makes Perfect!
Questions? Problems? Leave a comment and I’ll try my best to help.











Good math practice for my kid. Thanks
Way cool, some great points! I appreciate you making this post available, the rest of the site is also well done. I hope you have a wonderful day.
I just StumbledUpon this. Not bad. I’ll give it a thumbs up.